Matura z matematyki: Pewniaki, strategia i jak zdać na 100%

Przygotowanie do matury z matematyki na poziomie podstawowym może wydawać się wyzwaniem, ale z odpowiednim przewodnikiem staje się znacznie prostsze. Ten artykuł to kompleksowy zestaw informacji, który pomoże Ci zrozumieć zakres materiału, zidentyfikować kluczowe "pewniaki" maturalne oraz opracować skuteczną strategię nauki, która pozwoli Ci zdać egzamin z satysfakcjonującym wynikiem.

Matura z matematyki bez tajemnic: Jak wygląda egzamin i co cię czeka w arkuszu?

Egzamin maturalny z matematyki na poziomie podstawowym to sprawdzian twojej wiedzy i umiejętności, który trwa 180 minut. Arkusz egzaminacyjny został skonstruowany tak, aby w pełni ocenić Twoje przygotowanie łącznie możesz zdobyć 50 punktów. Kluczowe jest, abyś przekroczył próg 30%, co oznacza zdobycie co najmniej 15 punktów, aby zdać egzamin. Pamiętaj, że w arkuszu znajdziesz zarówno zadania zamknięte, jak i otwarte, które wymagają pokazania pełnego toku rozumowania.

Struktura egzaminu wygląda następująco:

• Czas trwania: 180 minut.
• Całkowita liczba punktów: 50.
• Próg zdawalności: 30% (minimum 15 punktów).
• Typy zadań: Zadania zamknięte (jednokrotnego wyboru, prawda/fałsz) oraz zadania otwarte.

Zadania zamknięte vs. otwarte: Gdzie najłatwiej zdobyć punkty?

Zadania zamknięte, takie jak te jednokrotnego wyboru czy typu prawda/fałsz, często pozwalają na szybkie zdobycie punktów. Wymagają one zazwyczaj rozpoznania poprawnej odpowiedzi spośród kilku podanych lub oceny prawdziwości stwierdzenia. Choć mogą wydawać się prostsze, nie należy ich lekceważyć, ponieważ stanowią znaczną część puli punktowej. Kluczowe jest tutaj dokładne czytanie poleceń i opcji odpowiedzi.

Zadania otwarte to z kolei szansa na wykazanie się pełnym zrozumieniem materiału i umiejętnością logicznego myślenia. Tutaj nie wystarczy wybrać gotową odpowiedź musisz samodzielnie dojść do rozwiązania, przedstawiając szczegółowy tok rozumowania, obliczenia i uzasadnienia. W zadaniach otwartych liczy się nie tylko wynik końcowy, ale przede wszystkim sposób, w jaki do niego dotarłeś. Nawet jeśli popełnisz drobny błąd rachunkowy, poprawne zastosowanie metod i strategii może przynieść Ci znaczną część punktów.

Kalkulator i tablice wzorów CKE: Twoi jedyni legalni pomocnicy na sali

Podczas egzaminu maturalnego z matematyki nie jesteś sam! Masz do dyspozycji kilka narzędzi, które mogą znacząco ułatwić Ci pracę. Przede wszystkim są to oficjalne "Wybrane wzory matematyczne" udostępnione przez Centralną Komisję Egzaminacyjną. Umiejętność sprawnego wyszukiwania i stosowania odpowiednich wzorów z tablic jest kluczowa dla efektywnego rozwiązania wielu zadań. Oprócz tego, możesz korzystać z linijki, cyrkla oraz prostego kalkulatora. Pamiętaj, że niedozwolone są kalkulatory naukowe czy programowalne.

Dozwolone pomoce naukowe to:

• "Wybrane wzory matematyczne" CKE.
• Cyrkiel.
• Linijka.
• Prosty kalkulator.

Fundament twojego sukcesu: Oficjalna lista wymagań CKE na maturę

Przygotowując się do matury, warto oprzeć się na oficjalnych wymaganiach egzaminacyjnych. Na rok 2026, podobnie jak w latach poprzednich, obowiązuje formuła oparta na informatorze CKE z 2023 roku. Oznacza to, że zakres materiału jest stabilny i przewidywalny, co daje Ci solidną podstawę do planowania nauki. Zrozumienie tych wymagań to pierwszy krok do sukcesu.

Liczby rzeczywiste i wyrażenia algebraiczne: Pierwszy krok do pewności siebie

Dział Liczby rzeczywiste i Wyrażenia algebraiczne stanowi fundament, na którym budowana jest dalsza wiedza matematyczna. Opanowanie tych zagadnień jest kluczowe dla zrozumienia bardziej złożonych tematów. Warto zwrócić szczególną uwagę na podstawowe operacje, własności liczb oraz przekształcanie wyrażeń.

Najważniejsze zagadnienia z tego działu to:

• Wzory skróconego mnożenia (kwadrat sumy, różnicy, różnica kwadratów).
• Potęgowanie i pierwiastkowanie własności działań.
• Logarytmy definicja i podstawowe własności.
• Działania na ułamkach algebraicznych.

Funkcje, czyli serce matury: Liniowa, kwadratowa i wykładnicza pod lupą

Funkcje to jeden z najważniejszych działów na maturze z matematyki, a funkcja kwadratowa stanowi jego absolutne serce. Musisz perfekcyjnie opanować jej własności: od obliczania delty, przez znajdowanie miejsc zerowych, po określanie współrzędnych wierzchołka paraboli. Kluczowe jest również umiejętne wyznaczanie wartości najmniejszej i największej funkcji w podanym przedziale oraz rozwiązywanie nierówności kwadratowych. Poza funkcją kwadratową, nie zapomnij o solidnym opanowaniu funkcji liniowej i wykładniczej ich zrozumienie jest niezbędne do rozwiązania wielu zadań.

Szczegółowe wymagania dotyczące funkcji:

• Funkcja kwadratowa:
  • Obliczanie wyróżnika (delty) i miejsc zerowych.
  • Wyznaczanie współrzędnych wierzchołka paraboli.
  • Określanie, czy funkcja przyjmuje wartość najmniejszą czy największą w danym przedziale.
  • Rozwiązywanie nierówności kwadratowych.
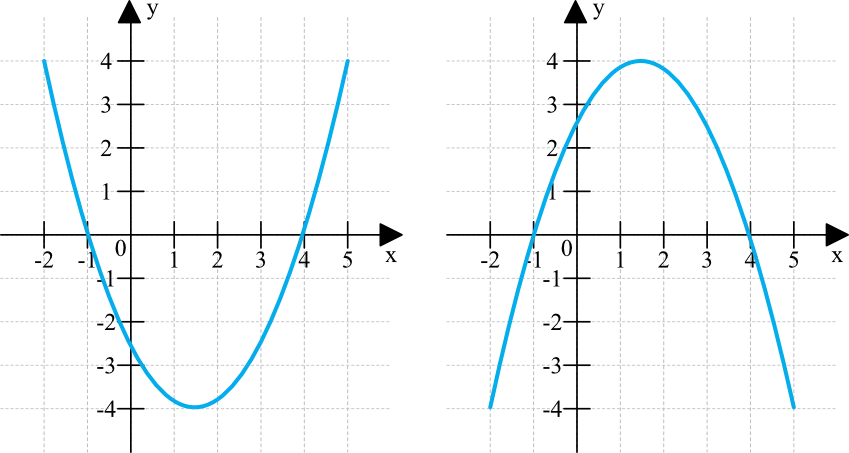
  • Interpretacja graficzna funkcji kwadratowej.
• Funkcja liniowa:
  • Wyznaczanie równania prostej przechodzącej przez dwa punkty.
  • Badanie monotoniczności funkcji liniowej.
  • Interpretacja geometryczna współczynnika kierunkowego.
• Funkcja wykładnicza:
  • Podstawowe własności funkcji wykładniczej.
  • Rozwiązywanie prostych równań wykładniczych.

Geometria nie taka straszna: Od planimetrii po stereometrię

Dział geometrii na maturze podstawowej obejmuje zarówno zagadnienia z geometrii płaskiej (planimetrii), jak i przestrzennej (stereometrii). W planimetrii skup się na solidnym opanowaniu własności figur płaskich, ze szczególnym uwzględnieniem trójkątów. Twierdzenie Pitagorasa, obliczanie pól różnych figur oraz podstawy trygonometrii w trójkącie prostokątnym to absolutna podstawa. Nie zapomnij również o zastosowaniu trygonometrii w zadaniach związanych z okręgiem.

Kluczowe zagadnienia z planimetrii:

• Własności trójkątów (różnoboczny, równoramienny, równoboczny, prostokątny).
• Twierdzenie Pitagorasa i jego zastosowania.
• Pola figur płaskich: trójkąta, kwadratu, prostokąta, rombu, trapezu.
• Podstawowe funkcje trygonometryczne (sinus, cosinus, tangens) w trójkącie prostokątnym.
• Własności okręgu i koła.

W stereometrii natomiast czeka Cię praca z bryłami. Musisz opanować obliczanie objętości i pól powierzchni podstawowych brył, takich jak graniastosłupy (w tym prostopadłościany i sześciany) oraz ostrosłupy (w tym ostrosłupy prawidłowe). Zrozumienie zależności między elementami tych brył jest kluczowe.

Kluczowe zagadnienia ze stereometrii:

• Podstawowe bryły obrotowe: walec, stożek, kula wzory na objętość i pole powierzchni.
• Graniastosłupy (w tym prostopadłościan i sześcian) wzory na objętość i pole powierzchni całkowitej.
• Ostrosłupy (w tym ostrosłupy prawidłowe) wzory na objętość i pole powierzchni całkowitej.

Ciągi, trygonometria i prawdopodobieństwo: Co jeszcze musisz opanować?

Oprócz funkcji i geometrii, na maturze pojawią się również inne ważne działy. Ciągi, zarówno arytmetyczne, jak i geometryczne, wymagają od Ciebie znajomości wzorów na n-ty wyraz oraz sumę początkowych wyrazów. Trygonometria skupia się na podstawowych tożsamościach i wartościach funkcji dla kątów ostrych. Nie można zapomnieć o podstawach kombinatoryki, rachunku prawdopodobieństwa i statystyki, które często pojawiają się w zadaniach praktycznych.

Kluczowe zagadnienia:

• Ciągi:
  • Ciąg arytmetyczny wzór na n-ty wyraz, wzór na sumę początkowych wyrazów.
  • Ciąg geometryczny wzór na n-ty wyraz, wzór na sumę początkowych wyrazów.
• Trygonometria:
  • Podstawowe tożsamości trygonometryczne.
  • Wartości funkcji trygonometrycznych dla kątów ostrych.
• Kombinatoryka, rachunek prawdopodobieństwa i statystyka:
  • Podstawowe pojęcia kombinatoryki (permutacje, kombinacje, wariacje).
  • Obliczanie prawdopodobieństwa zdarzeń.
  • Podstawowe miary statystyczne (średnia, mediana, dominanta).

Pewniaki maturalne: Na tych działach skup się najbardziej, by zagwarantować sobie 30%!

Analiza arkuszy maturalnych z poprzednich lat jednoznacznie wskazuje, że pewne działy i typy zadań pojawiają się niemal co roku. Skupienie się na tych "pewniakach" to najskuteczniejsza strategia, aby zagwarantować sobie zdobycie wymaganego progu 30 punktów. Nie chodzi o to, by znać wszystko na pamięć, ale by perfekcyjnie opanować te zagadnienia, które z największym prawdopodobieństwem pojawią się na egzaminie.

Funkcja kwadratowa: Dlaczego musisz ją umieć perfekcyjnie?

Funkcja kwadratowa to absolutny król matury z matematyki na poziomie podstawowym. Zadania z tego działu pojawiają się niemal w każdym arkuszu i często stanowią znaczną część puli punktowej. Ich opanowanie jest kluczowe nie tylko dla zdania egzaminu, ale również dla osiągnięcia wyższego wyniku. Musisz być biegły w obliczaniu delty, znajdowaniu miejsc zerowych, określaniu współrzędnych wierzchołka paraboli, a także w rozwiązywaniu nierówności kwadratowych. Pamiętaj, że często pojawiają się też zadania wymagające wyznaczenia wartości najmniejszej lub największej funkcji w danym przedziale.

Umiejętności, które musisz posiadać:

• Precyzyjne obliczanie delty i miejsc zerowych funkcji kwadratowej.
• Poprawne wyznaczanie współrzędnych wierzchołka paraboli.
• Określanie, czy funkcja przyjmuje wartość najmniejszą czy największą w podanym przedziale.
• Skuteczne rozwiązywanie nierówności kwadratowych.
• Interpretacja graficzna funkcji kwadratowej.

Procenty w zadaniach praktycznych: Pewne punkty z lokat i obniżek

Kolejnym pewniakiem są zadania z procentami. Pojawiają się one zazwyczaj w kontekstach praktycznych, takich jak obliczenia związane z lokatami bankowymi, kredytami, obniżkami cen czy podwyżkami podatków. Choć mogą wydawać się proste, wymagają precyzji i zrozumienia, jak działają procenty w różnych sytuacjach. Zadania te są doskonałą okazją do zdobycia łatwych punktów, pod warunkiem, że potrafisz szybko zidentyfikować, o co dokładnie pytają.

Przykłady zastosowań procentów:

• Obliczenia procentowe (np. podatek, marża).
• Zmiany procentowe (wzrost, spadek).
• Zadania związane z lokatami i kredytami.
• Obliczanie rabatów i podwyżek cen.

Geometria analityczna: Jak bezbłędnie operować na prostych i okręgach?

Geometria analityczna to dział, który łączy wiedzę o geometrii z umiejętnością posługiwania się układem współrzędnych. Na maturze często pojawiają się zadania dotyczące równania prostej, warunków na proste równoległe i prostopadłe, obliczania odległości między punktami oraz równania okręgu. Kluczem do sukcesu jest tutaj znajomość odpowiednich wzorów i umiejętność ich zastosowania.

Kluczowe zagadnienia z geometrii analitycznej:

• Wyznaczanie równania prostej przechodzącej przez dwa punkty.
• Warunki równoległości i prostopadłości prostych.
• Obliczanie odległości między dwoma punktami na płaszczyźnie.
• Wyznaczanie równania okręgu.

Ciąg arytmetyczny i geometryczny: Sprawdzone schematy zadań, które powtarzają się co roku

Ciągi arytmetyczne i geometryczne to kolejne działy, które można uznać za "pewniaki". Zadania dotyczące tych ciągów zazwyczaj opierają się na sprawdzonych schematach. Najczęściej pojawiają się pytania o obliczenie konkretnego wyrazu ciągu (n-tego) lub o wyznaczenie sumy jego początkowych wyrazów. Perfekcyjne opanowanie wzorów na te elementy pozwoli Ci zdobyć cenne punkty bez większych trudności.

Typowe zadania dotyczące ciągów:

• Obliczanie n-tego wyrazu ciągu arytmetycznego.
• Obliczanie sumy początkowych wyrazów ciągu arytmetycznego.
• Obliczanie n-tego wyrazu ciągu geometrycznego.
• Obliczanie sumy początkowych wyrazów ciągu geometrycznego.

Strategia nauki, która działa: Jak mądrze zaplanować powtórki?

Wielu uczniów czuje się przytłoczonych ilością materiału do opanowania przed maturą. Kluczem do sukcesu nie jest jednak uczenie się wszystkiego na ostatnią chwilę, ale mądre i strategiczne zaplanowanie powtórek. Systematyczność, powtarzanie kluczowych zagadnień i praktyka to fundamenty skutecznej nauki. Pamiętaj, że celem jest nie tylko zdanie egzaminu, ale również zbudowanie pewności siebie, która pozwoli Ci spokojnie podejść do każdego zadania.

Dlaczego rozwiązywanie starych arkuszy CKE to najlepsza metoda nauki?

Rozwiązywanie arkuszy maturalnych z poprzednich lat to jedna z najskuteczniejszych metod przygotowania do egzaminu. Pozwala ona nie tylko na oswojenie się z formatem i typem zadań, ale także na naukę efektywnego zarządzania czasem podczas egzaminu. Co więcej, analiza własnych błędów popełnionych podczas rozwiązywania tych arkuszy pozwala na szybką identyfikację słabych punktów i ukierunkowanie dalszej nauki. Jest to również doskonały sposób na powtórzenie "pewniaków" maturalnych w praktycznym kontekście.

Korzyści z rozwiązywania starych arkuszy:

• Oswojenie się z formatem i strukturą egzaminu.
• Nauka efektywnego zarządzania czasem.
• Identyfikacja własnych słabych punktów i obszarów do poprawy.
• Powtarzanie kluczowych zagadnień i "pewniaków" w praktyce.
• Budowanie pewności siebie przed egzaminem.

Najczęstsze błędy maturzystów: Jak ich uniknąć i nie tracić cennych punktów?

Wielu maturzystów popełnia podobne błędy, które mogą kosztować ich cenne punkty. Do najczęstszych należą błędy rachunkowe, wynikające z pośpiechu lub nieuwagi. Bardzo ważne jest również pamiętanie o zapisywaniu toku rozumowania w zadaniach otwartych nawet jeśli wynik jest poprawny, brak zapisu może skutkować utratą punktów. Często problemem jest także nieuważne czytanie poleceń, co prowadzi do rozwiązywania zupełnie innego zadania niż to, które zostało postawione. Niewłaściwe korzystanie z tablic wzorów czy problemy z zarządzaniem czasem to kolejne pułapki, na które należy uważać.

Najczęstsze błędy i wskazówki, jak ich unikać:

• Błędy rachunkowe: Dokładnie sprawdzaj swoje obliczenia, szczególnie te wykonywane "w pamięci".
• Brak zapisu toku rozumowania: Zawsze przedstawiaj wszystkie kroki rozwiązania w zadaniach otwartych.
• Nieuważne czytanie poleceń: Przeczytaj polecenie dwa razy, upewnij się, że rozumiesz, o co pytają.
• Niewłaściwe korzystanie ze wzorów: Upewnij się, że stosujesz właściwy wzór i poprawnie podstawiasz dane.
• Problemy z czasem: Ćwicz rozwiązywanie arkuszy na czas.
• Stres i panika: Stosuj techniki relaksacyjne, pamiętaj o swoim przygotowaniu.

Plan działania krok po kroku: Od teorii do praktyki w ostatnich miesiącach przed maturą

Oto propozycja planu działania, który pomoże Ci efektywnie przygotować się do matury w ostatnich miesiącach:

1. Powtórka teorii (pierwszy miesiąc): Systematycznie przypominaj sobie definicje, wzory i twierdzenia z poszczególnych działów. Skup się na zrozumieniu materiału, a nie tylko na zapamiętywaniu.
2. Rozwiązywanie zadań (drugi miesiąc): Po każdej powtórzonej partii teorii rozwiązuj zadania z podręczników i zbiorów zadań, zaczynając od prostszych, a kończąc na trudniejszych.
3. Skupienie na "pewniakach" (trzeci miesiąc): Poświęć dodatkowy czas na utrwalenie zagadnień, które najczęściej pojawiają się na maturze.
4. Praktyka z pełnymi arkuszami (czwarty miesiąc): Rozwiązuj pełne arkusze maturalne z poprzednich lat na czas. Symuluj warunki egzaminacyjne.
5. Analiza błędów i powtórki (ciągłe): Po każdym rozwiązanym arkuszu dokładnie analizuj swoje błędy i wracaj do tych zagadnień, które sprawiają Ci najwięcej trudności.

Co jeśli celem jest więcej niż 30%? Jakie tematy decydują o wysokim wyniku?

Jeśli Twoim celem jest wynik znacznie powyżej progu zdawalności, musisz wyjść poza utarte schematy i zmierzyć się z trudniejszymi zadaniami. Oprócz perfekcyjnego opanowania podstaw, kluczowe staje się rozwijanie umiejętności analitycznego myślenia i rozwiązywania problemów, które wymagają głębszego zrozumienia materiału. Zadania na dowodzenie, zadania optymalizacyjne oraz te wymagające nieszablonowego podejścia to właśnie te, które decydują o wysokim wyniku.

Zadania na dowodzenie: Jak poprawnie konstruować argumentację?

Zadania na dowodzenie to test Twojej zdolności do logicznego i spójnego argumentowania. Wymagają one nie tylko znajomości twierdzeń, ale także umiejętności poprawnego ich zastosowania i przedstawienia krok po kroku. Pamiętaj, aby Twoja argumentacja była precyzyjna, zawierała wszystkie niezbędne założenia i wnioski, a także była poprawna matematycznie. Często kluczem jest tutaj dobre zrozumienie definicji i twierdzeń.

Zadania optymalizacyjne: Klucz do maksymalnej liczby punktów w zadaniach otwartych

Zadania optymalizacyjne, często związane ze znajdowaniem wartości największej lub najmniejszej, to prawdziwy sprawdzian umiejętności rozwiązywania problemów. Sukces w nich polega na umiejętnym przełożeniu treści zadania na język matematyki, zbudowaniu odpowiedniego modelu (często funkcji) i wykorzystaniu narzędzi matematycznych do znalezienia optymalnego rozwiązania. Perfekcyjne opanowanie funkcji kwadratowej jest tutaj nieocenione.

Przeczytaj również: Matura z informatyki: Czy jest trudna? Analiza i strategie sukcesu

Nieszablonowe myślenie: Gdzie szukać dodatkowych punktów, gdy opanujesz już podstawy?

Aby zdobyć naprawdę wysoki wynik, musisz rozwijać swoje nieszablonowe myślenie matematyczne. Nie ograniczaj się do mechanicznego zapamiętywania wzorów. Staraj się zrozumieć, dlaczego dane twierdzenie działa, skąd się biorą wzory i jak można je zastosować w nietypowych sytuacjach. Zachęcam do eksperymentowania z zadaniami, szukania alternatywnych rozwiązań i głębszego analizowania problemów. To właśnie te umiejętności pozwalają zdobyć dodatkowe punkty w trudniejszych zadaniach, które odróżniają najlepszych.